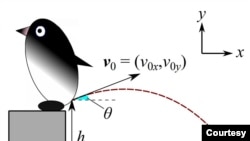
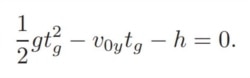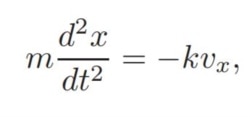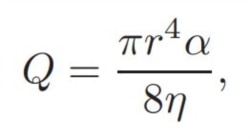Nếu chỉ nhìn hình, quý vị sẽ nghĩ con chim cánh cụt này đang làm gì?
Quý vị nghĩ ra rồi thì để đó nhe, để tôi đọc bài báo cho chắc ăn.
Nếu quý vị có đọc bài, thì sau khi đọc quý vị sẽ thấy rằng thực ra câu trả lời của quý vị ... quả đúng là như vậy. Con chim cánh cụt nó đang đi cầu.
Đến đây tôi xin khuyến cáo quý độc giả nào dị ứng với việc nói chuyện tiêu hóa xin ngừng đọc ngay. Tìm bài nào khác nói chuyện trời trăng mây nước hoa lá cành xinh tươi đẹp đẽ mà đọc.
Bài báo toán trên chưa được đăng chính thức, chỉ mới đưa lên mạng dưới dạng “preprint.” Preprint là khi một nhà khoa học viết xong một bài báo, tuy chưa được nhận đăng nhưng cũng đưa lên cho mọi người đọc, với mục đích lấy phản hồi. Nếu lỡ có lỗi gì thì có người thấy, còn kịp sửa. Nếu có hướng phát triển nào cũng có thể phát triển được và bài sẽ có giá trị hơn.
Đăng pre-print trên mạng do đó có lợi cho tất cả các bên. Về phía tác giả, nếu là sáng kiến mới thì do đăng pre-print, mọi người đều biết ai là người nghĩ ra sáng kiến đó trước. Về phía báo chuyên ngành, người duyệt bài và góp ý bài sẽ có bài chất lượng cao hơn, đỡ phải nhức đầu với bài kém, bài lỗi. Với cộng đồng khoa học nói chung, bài preprint được đưa lên mạnng sớm, sẽ giúp cho các nhà nghiên cứu được cập nhật với tiến bộ mới nhanh hơn. Thí dụ tôi đang nghiên cứu về A và có ai đó làm được bước tiến bộ B mà có thể giúp được tôi. Nếu tôi chỉ có thông tin từ các tạp chí chuyên môn, thì tùy ngành có thể thông tin sẽ tới 1 hoặc 2 năm sau khi bước B đã thực hiện xong. Trong khi nếu B được đưa lên preprint trước, tôi có thể (tạm) sử dụng thông tin đó sớm hơn tới 1, 2 năm.
Thế thì con chim cánh cụt này xuất hiện trong bài preprint của hai nhà khoa học Nhật Bản, Hiroyuki Tajima khoa Toán Lý đại học Kochi, và Fumiya Fujisawa thuộc viện hải dương Katsurahama Aquarium, cũng ở Kochi.
Đọc bài preprint này tôi mới biết con chim cánh cụt không đại tiện như các con vật khác. Phân của chim cánh cụt không rớt thẳng xuống đất như phân các con khác. Lý do được giải thích là con chim cánh cụt nhưng chỉ cánh nó cụt mà chân nó cũng cụt. Phân mà rớt thẳng xuống sẽ rớt trúng chân, dây vào bụng, gây đủ loại bệnh tật. Trong quá trình tiến hóa, thiên nhiên đã ưu đãi những con nào mà không suốt ngày dẫm lên phế phẩm chính nó.
Cho nên ngày nay, con chim cánh cụt có đặc điểm là nó đứng ở đây nhưng ... ị ở chỗ khác! Khi phóng uế, con chim cánh cụt bắn phân ra xa trung bình 0.4 mét, tức là xấp xỉ chiều cao của chính nó. Tajima và Fujisawa so sánh là nếu cùng cách đó, “một người cao 1m7 đi đại tiện sẽ bắn bay 1m7.”
Bài báo khởi đầu với những công thức toán quen thuộc. Thí dụ như công thức này nhiều vị độc giả có thể nhận ra từ lớp Vật Lý trung học.
Hoặc công thức này, trong lớp Giải Tích hay Vật Lý đại học.
Hoặc công thức này, thường thường phải ai chuyên ngành Vật Lý hay Cơ Khí và học lớp cơ học thủy khí (fluid dynamics, còn gọi là cơ học chất lưu) mới học tới.
Nói chung là phân tích chuyện đi giải cũng lắm công phu.
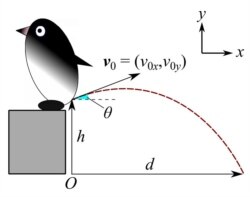
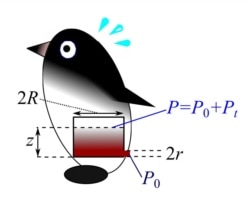
Đây là mô hình của hệ thống bệ phóng của con chim cánh cụt, một thứ đại bác bắn hơi, trong đó bom được bắn ra bằng áp suất của trực tràng, được thể hiện một cách toán học bằng tổng của hai áp suất P0 của khí quyển vả Pt của riêng trực tràng.
Phân tích mô hình này, Tajima và Fujisawa ước tính ra áp suất Pt của trực tràng con chim cánh cụt cao hơn người ta tưởng, cao gần gấp rưỡi ước tính trước đây.
Và hơn nữa, với áp suất trực tràng cao như vậy, Tajima và Fujisawa cho biết khoảng cách tối đa con chim cánh cụt có thể đạt được khi đánh bom tấn là tới 1.34m.
Tính theo đơn vị Mỹ, 1.34 mét là 4 feet 4. Vậy bây giờ biết rồi. Nếu giãn cách xã hội 6 feet như người ta khuyên, thì giao du với chim cánh cụt rất an toàn.
Người ta nói toán học áp dụng được tất cả mọi nơi, quả không sai.